После отъезда Бартельса из Казани все преподавание «чистой математики» переходит к Лобачевскому. Со следующего года, по возвращении Симонова из его плавания (1821), для Лобачевского отпала необходимость, а может быть и желательность, чтения курсов по астрономии; в 1821 г. оно как бы обрывается. В ближайшие следующие годы (нам неизвестно в точности, как и когда) слагается его великое новое слово, его система неевклидовой геометрии1. Первое сообщение о ней было сделано Лобачевским Казанскому университету 11/23 февраля 1826 г. Рукопись этого доклада Лобачевского утеряна, но через три года в «Казанском вестнике» публикуется его основоположная работа «О началах геометрии»2. Здесь новая часть, добавленная, судя по примечанию Лобачевского, к работе 1826 г., начинается со следующих знаменательных слов:
«Изложенная нами теория параллельных предполагает линии с углами в такой зависимости, которая, как после увидим, находится или нет в природе, доказать никто не в состоянии...».
Но почему же, — должен был поставить вопрос вдумчивый читатель «Казанского вестника», если бы таковой читатель тогда нашелся, — мы должны отказаться от возможности проверки новой геометрии в опыте и в наблюдении? Разве мы потеряли веру в лапласову установку о всепобеждающей силе разума? Или разве сам Лобачевский в те же годы (точнее в 1828 г.) не говорил об этом в своей «Речи о важнейших предметах воспитания»:
«Чему, спрашиваю я, одолжены своими блистательными успехами в последнее время математические и физические науки, слава нынешних веков, торжество ума человеческого?»3
Так почему же как раз на вопросе о действительности новой геометрии кончается это торжество?
Чтобы обосновать свое утверждение, Лобачевский обращается к простейшим геометрическим образам — к плоским треугольникам и к измерению суммы их углов. Напомним, что всего за год до появления в печати работы Лобачевского Гаусс в своих геометрических исследованиях тоже обращался к измерению суммы углов в треугольниках, но только в треугольниках земных; его знаменитые «Общие исследования о кривых поверхностях» (1828)4 как-то неожиданно заканчивается примером, взятым из той триангуляции, в обработке которой сам Гаусс участвовал. Этот пример относится, как говорит Гаусс, к «самому большому треугольнику, который был измерен в предыдущие годы». Уравнивая и вычисляя углы этого треугольника с исключительной точностью до 10-5 сек. дуги, Гаусс показывает, что сумма их, после надлежащих — гауссовых — редукций к плоскости, приводится с этой точностью ровно к 180°. Таким образом, в земных треугольниках уклонений от обычной геометрии не наблюдается5.
Но Лобачевский идет теперь дальше, и — мы могли бы сказать словами Галилея — «оставив в стороне земное, обращается к небесному». Однако в ту пору наука о небе оставалась еще в полной неизвестности по основному вопросу мироздания — о расстоянии Солнца до ближайших звезд. Идет ли свет от них месяцы, или годы, или десятилетия, — никто не мог еще сказать. Но это важнейший вопрос для Лобачевского. Он пишет: «Кажется, более всего можно полагаться на способ, придуманный Дасса-Мондидье», — и ссылается на статью этого никому не известного автора, помещенную во французском «Астрономическом ежегоднике на 1831 г.»6.
Необходимо прежде всего обратить внимание на ту тщательность, с которой Лобачевский изучал современную ему астрономическую литературу. Ежегодник, о котором идет речь, был опубликован в Париже в 1828 г. и, очевидно, не сразу попал в Казанскую библиотеку; но уже в 1829 г. Лобачевский публикует свои «Начала геометрии», в которых данные французского астронома полагаются в основу проверки действительности неевклидовой геометрии в космических пространствах. И неважно для нас, хорош или плох был способ определения звездных параллаксов, придуманный отставным французским моряком, который в течение четырех лет неустанно вел наблюдения, — правда, примитивные по технике, — для определения параллаксов трех звезд: 29-й Эридана, Ригеля и Сириуса. Для нас существенно здесь то, что в первый раз за историю человеческой культуры уединенный геометр и мыслитель в далекой Казани делает попытку именно из этих наблюдений вывести свойства пространства и геометрии мира! Для упомянутых трех звезд французский моряк-астроном получил параллаксы7: 1",00 для 29-й Эридана, 0",72 для Ригеля и 0",62 для Сириуса.
Как мы теперь знаем, это все определения завышены и нереальны; параллакс первой из этих звезд не определен до настоящего времени; для Ригеля он оказался равным 0",006, но с вероятной ошибкой ±0"0078; для Сириуса — одной из самых близких звезд — он равен 0",371 ± 0",004. Но вместе с тем мы знаем, что наибольший измеренный параллакс равен 0",76. Таким образом, в смысле порядка величины наибольших параллаксов результаты Дасса можно считать приемлемыми. Но Лобачевский опирается на них, чтобы выяснить, какова наименьшая величина измеренных параллаксов, так как ему требуется знать расстояние до самой далекой звезды. И тут, со всей строгостью естествоиспытателя, который принимает лишь то, что получено в опыте и наблюдении, Лобачевский считает, что 0",62, определенные Дасса, это и есть наименьший параллакс, т. е. он принимает, что свет идет к Земле от самой далекой звезды 5½ лет; затем он приступает к своим выводам.
Здесь, на наш взгляд, уместно подчеркнуть особенность его постановки задачи; во множестве курсов астрономии параллакс определяется как «угол при звезде» в том треугольнике, основанием которого служит радиус земной орбиты, а звезда является третьей вершиной. Но угла при звезде никто никогда наблюдать не будет: он выводится, конечно, через сумму обоих других углов. Лобачевский поступает гораздо рациональнее: он определяет параллакс как полуразность направлений на звезду из двух противоположных точек земной орбиты. Угол при звезде остается великой неизвестной: если сумма трех углов треугольника меньше двух прямых и равна π – 2ω, то дефект 2ω ляжет на угол при звезде, недоступный нашему измерению. Таким образом, у Лобачевского схема всегда такая, как показано на рис. 2.
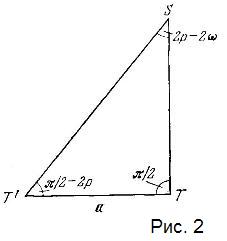 Здесь а — диаметр земной орбиты, Т и Т' — два диаметрально противоположных положения Земли, S — положение звезды. Солнце, не показанное на рисунке, лежит в середине отрезка ТТ'; угол при звезде равен 2p–2ω. Заметим, что комментаторы Лобачевского не всегда отчетливо поясняют эту схему. Один из них9 говорит, что она изображает треугольник между Солнцем, звездой и Землей, что неверно, так как основание треугольника — диаметр, а не радиус земной орбиты; в другом месте10 мы читаем, что угол при Т предполагается прямым «для простоты рассуждений»; это тоже неверно, так как схема Лобачевского приложена ко всякой звезде в тот момент, когда она находится в квадратуре11 с Солнцем, как это и поясняет затем Лобачевский.
Здесь а — диаметр земной орбиты, Т и Т' — два диаметрально противоположных положения Земли, S — положение звезды. Солнце, не показанное на рисунке, лежит в середине отрезка ТТ'; угол при звезде равен 2p–2ω. Заметим, что комментаторы Лобачевского не всегда отчетливо поясняют эту схему. Один из них9 говорит, что она изображает треугольник между Солнцем, звездой и Землей, что неверно, так как основание треугольника — диаметр, а не радиус земной орбиты; в другом месте10 мы читаем, что угол при Т предполагается прямым «для простоты рассуждений»; это тоже неверно, так как схема Лобачевского приложена ко всякой звезде в тот момент, когда она находится в квадратуре11 с Солнцем, как это и поясняет затем Лобачевский.
Установив эти определения, Лобачевский доказывает три теоремы — три следствия из его геометрической системы. Первая и важнейшая из них гласит: как бы ни было велико расстояние звезды от Солнца, ее параллакс остается больше некоторой абсолютной постоянной.
Эта основная теорема создает впечатление, что астрономы, получая параллаксы все более далеких звезд, будут приближаться к познанию этой абсолютной постоянной, а следовательно, и к выяснению метрических свойств пространства. На самом деле это не так: на этом пути структура пространства ускользает от астрономов, и вот почему: та постоянная, о которой здесь идет речь, есть отношение вполне определенной длины, именно диаметра земной орбиты, к той единице длины, которой в геометрии Лобачевского измеряются все длины вообще, так же как в обычной геометрии все углы измеряются в долях окружности единичного радиуса.
Пусть k — это абсолютная единица длин; р — параллакс звезды, выраженный в секундах дуги; а — диаметр земной орбиты. Тогда теорема Лобачевского имеет только тот смысл, что12
k > 206 265 а/2р. (1)
Следовательно, если в наши дни астрономы определяют у какой-либо звезды параллакс в 0",05, то они могут только сказать, что абсолютная единица длин у Лобачевского в 2 · 106 раз больше диаметра земной орбиты; а так как никакие пределы для постоянной k не могут быть назначены и она ни с какими другими постоянными, нам известными из опыта, не связана, то к познанию нижнего предела всех параллаксов астрономические определения никогда не приведут13.
Едва ли можно было бы в форме более глубокой и отчетливой сочетать две истины, казалось бы друг другу совершенно противоречащие: пространство бесконечно, но параллаксы всех звезд, его населяющих, как бы они ни были далеки, не могут быть меньше некоторой определенной величины.
Лобачевский подчеркивает это изумительное положение вещей в следующих словах:
«Между тем нельзя не увлекаться мнением Лапласа, что видимые нами звезды и Млечный путь принадлежат к одному только собранию небесных светил, подобных тем, которые усматриваем как слабо мерцающие пятна в созвездиях Ориона, Андромеды, Козерога и пр. Итак, не говоря о том, что в воображении пространство может быть продолжаемо неограниченно, сама природа указывает нам такие расстояния, в сравнении с которыми исчезают за малостью даже расстояния нашей Земли до неподвижных звезд»14.
Эти грандиозные расстояния нам даны природой, но они еще не измерены; наибольшим измеренным расстоянием остается для Лобачевского то, которое соответствует звездному параллаксу р = 0",62. Но вот именно потому, что сама природа раскрывает нам такие расстояния, перед которыми ничтожны расстояния, определяемые только что указанными звездными параллаксами, человечество не в состоянии решить, какая геометрия — обыкновенная или геометрия Лобачевского — адекватна природе космоса. Астрономический опыт определения расстояний звезд решить этого не может. Но такое утверждение в устах Лобачевского отнюдь не есть признание принципиальной непознаваемости геометрии мира. Нет, Лобачевский далек от этого. Здесь уместно вспомнить слова А. М. Ляпунова, затерянные в примечании к его очерку о П. Л. Чебышеве:
«Великий геометр, подобно П. Л. Чебышеву, оставался всегда на реальной почве и в этих изысканиях трансцендентального15 характера едва ли мог увидеть развитие своих идей»16. Разумеется, реальная первопричина невозможности решения вопроса о космической геометрии состоит в том, что астрономы не имеют способов измерять угол при звезде в треугольнике, основание которого есть диаметр земной орбиты. Но дальше Лобачевский в известной мере обходит и это роковое затруднение, доказывая свою вторую, весьма замечательную теорему: если определены параллаксы двух звезд, находящихся на различных расстояниях от Солнца, то можно определить верхнюю границу дефекта 2ω в том треугольнике, у которого основание — диаметр земной орбиты, а вершина — при более близкой звезде.
Пусть р' — параллакс более далекой, р — параллакс более близкой звезды; тогда, по теореме Лобачевского17,
ω< 2p sin2 x/2, (2)
где sin x = р'/р.
Для численной иллюстрации обозначим
р'/р = n, 2p sin2 x /2 = β,
так что в силу формулы (2)
ω< p β.
Значения β по аргументу n приведены в следующей таблице:
|
n |
β |
n |
β |
|
0,1 |
0,009 |
0,5 |
0,134 |
|
0,2 |
0,020 |
0,6 |
0,200 |
|
0,3 |
0,046 |
0,7 |
0,286 |
|
0,4 |
0,084 |
0,8 |
0,402 |
|
0,5 |
0,134 |
0,9 |
0,710 |
Лобачевский, опираясь все на те же данные из статьи Дасса, полагает р' = 0",62, р = 1",00; тогда n = 0,62, β = 0,217. Следовательно, в треугольнике, «который простирается до второй из сих звезд», с параллаксом в 1",
2ω < 0",43,
как и дано у Лобачевского.
Но если мы примем за меньший параллакс р = 0",05, а за наибольший р = 0",75, то по формуле (2) получим, что
2ω < 0",0033.
Таким образом, с теми данными, которыми мы теперь располагаем, можно утверждать, что дефект космических треугольников с вершиной у звезды не превышает нескольких тысячных долей секунды дуги.
Замечательно здесь то, что вторая, далекая звезда действует как бы как некоторый светоч, освещающий геометрию малого треугольника, простирающегося до близкой звезды. Чем эта вторая звезда дальше, тем меньше будет дефект малого треугольника; вот почему для Лобачевского имеет столь большое значение самый малый известный параллакс для земного диаметра; чем он меньше, тем меньше дефекты в треугольниках с вершиной в любой более близкой звезде.
Третья теорема Лобачевского относится к тому воображаемому случаю, когда звезда находилась бы от Земли на расстоянии диаметра земной орбиты (именно TS = а на рис. 2), т. е. к треугольнику, оба катета которого были бы равны 2 · 150 ·106 км; эта теорема есть следствие общей формулы Лобачевского для дефекта ω и той оценки, которая содержится в теореме 1. Лобачевский получает из них неравенство
ω < р' 2 sin 1". (3)
Здесь р' есть снова наименьший измеренный с Земли параллакс, т. е. наименьший параллакс для диаметра земной орбиты а ; за таковой Лобачевский принимает опять р' = 0",62 и получает:
2ω < 3",72 · 10–6.
К несчастью, Лобачевский совершил численную ошибку или допустил опечатку; у него написано в «Началах геометрии»18:
2ω < 3",72 · 10–4.
Но и при этой численной ошибке Лобачевский убеждается, что в пределах Солнечной системы уклонения от условий обычной геометрии могут быть лишь чрезвычайно малы.
- 1. О первых работах Лобачевского по неевклидовой геометрии см. в упомянутой уже книге В. Ф. Кагана (изд. 2-е, 1948 г.), стр. 176 — 184.
- 2. Это произведение Лобачевского переиздано теперь в 1-м томе Полного собрания его сочинений (ГТТИ, 1946, стр. 179 — 411) с вводной статьей и комментарием А. П. Котельникова; для нашего дальнейшего изложения особенно важны стр. 207 — 210 текста и стр. 283 — 286 Примечаний.
- 3. Л. Б. Модзалевский, ук. соч., стр. 321 — 327; цитируемое место на стр. 323.
- 4. Имеется русский перевод Краснова, под ред. проф. К. А. Поссе, СПб., 1887; подлинник (по-латыни) в IV томе Полного собрания трудов Гаусса (Gauss Werke, Bd. IV., S. 217 — 258).
- 5. Гаусс говорит: «Так, например, в самом большом из треугольников, которые мы измеряли в прошлые годы, а именно между точками Гогегаген, Броккен, Инзельсберг, где избыток суммы углов был 14",85348, вычисление дало следующие величины для приведения углов (от эллипсоида) к плоскости: –4",95113; –4",95104; –4",95131». Сумма этих редукций составляет как раз –14",85348, так что сумма углов плоского треугольника есть 180°, с точностью до 10–5 сек. дуги.
- 6. «Connaissance des Temps pour l’аn 1831». Paris, 1828, p 120 — 148. Полное название этой работы: «Дасса-Мондидье. Мемуар об определении параллакса и собственного движения звезд по склонению посредством нового способа искусственных покрытий». В приложенном отчете об этой работе (стр. 149 — 151) Делямбр указывает на связь ее с некоторыми важными соображениями Галилея об определении звездных параллаксов.
- 7. Сказать, что параллакс звезды равен 1", — то же самое, что сказать, что свет от нее идет к нам 4/3 года.
- 8. Эти сведения справедливы на момент написания статьи, т. е. для 1949 года. В настоящее время, например, параллакс Ригеля известен с довольно высокой точностью, он равен 0",00378±0",00034. — Прим. админа.
- 9. Н. И. Лобачевский. Полн. собр. соч., т. 1. Комментарий, стр. 284.
- 10. Н. Liebmann. Nichteuclidische Geometrie, 1905, стр. 244. Существенно правильнее у Богомолова — «Основания геометрии», 1923, стр. 310. Чтобы показать соответствие схемы Лобачевского с обычными построениями сферической астрономии, представим на рисунке плоскость эклиптики Е.
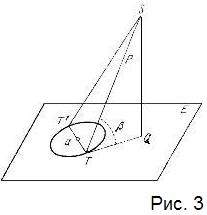 Пусть Q есть основание перпендикуляра, опущенного на эту плоскость из звезды S. Проведем из Q касательную QТ к кругу, представляющему земную орбиту; если проведем еще плоскость Р через прямые SQ и QT, то эта плоскость будет касательной к прямому цилиндру, основанием которого служит орбита Земли; поэтому диаметр TТ' будет перпендикулярен к прямой TS; точки Т, S, Т' как раз и образуют треугольник Лобачевского на рис. 2. (Аналогичное построение в том случае, когда Q попадает внутрь земной орбиты.) Пусть теперь р — параллакс звезды; λ' и λ — ее гелиоцентрическая и и геоцентрическая долготы; β — ее широта, т. е. угловое возвышение над плоскостью эклиптики. По формулам сферической астрономии для параллакса по долготе имеем:
Пусть Q есть основание перпендикуляра, опущенного на эту плоскость из звезды S. Проведем из Q касательную QТ к кругу, представляющему земную орбиту; если проведем еще плоскость Р через прямые SQ и QT, то эта плоскость будет касательной к прямому цилиндру, основанием которого служит орбита Земли; поэтому диаметр TТ' будет перпендикулярен к прямой TS; точки Т, S, Т' как раз и образуют треугольник Лобачевского на рис. 2. (Аналогичное построение в том случае, когда Q попадает внутрь земной орбиты.) Пусть теперь р — параллакс звезды; λ' и λ — ее гелиоцентрическая и и геоцентрическая долготы; β — ее широта, т. е. угловое возвышение над плоскостью эклиптики. По формулам сферической астрономии для параллакса по долготе имеем:(λ' – λ) соs β = p sin (☼ – λ),
где ☼ — долгота Солнца. Пусть для положения Земли в Т долгота Солнца равна ☼1, долгота звезды — λ1, причем
☼1 – λ1 = π/2,
и, аналогично, для положения Земли в Т'
☼2 – λ2 = 3π/2.
Учитывая, что широта β и гелиоцентрическая долгота звезды λ' в обоих случаях одинаковы, получим:
(λ2 – λ1) cos β = 2р,
что и соответствует схеме Лобачевского.
- 11. Т. е. когда разность долгот и Солнца и звезды равна 90°.
- 12. Численный множитель в формуле (1) есть величина, обратная sin 1".
- 13. Эта первая теорема Лобачевского есть простое следствие из основных положений его геометрической системы. В Комментарий А. П. Котельникова (т. 1, стр. 283) вкралась ошибка: в 4-й формуле примечания 26-го, в правой части неравенства, пропущен множитель 2, так что окончательный результат должен быть a < tg2p, как в тексте Лобачевского (там же, стр. 207).
- 14. По-видимому, Лобачевский имеет в виду следующее место из «Exposition du Systéme du Monde» (Oeuvres, v. VI, p. 455): «Таким образом, вероятно, что среди туманностей многие представляют собой скопления очень большого числа звезд и что, если смотреть на них изнутри, они представились бы подобными Млечному Пути. Если теперь вдуматься в это изобилие звезд и туманностей, рассеянных в небесных пространствах, и в те огромные расстояния, которыми они отделены, то воображение, изумленное огромностью Вселенной, не сможет постичь его границ». Эта последняя фраза Лапласа как раз соответствует высказыванию Лобачевского: «В воображении пространство может быть продолжаемо неограниченно».
- 15. Т. е. лежащих за пределами возможного опыта.
- 16. Этот очерк А. М. Ляпунова включен в издание: «П. Л. Чебышев. Избранные математические труды. ОГИЗ, 1946» (см. стр. 20).
- 17. Доказательство этой теоремы довольно сложно; оно прекрасно разъяснено А. П. Котельниковым в упомянутом Комментарии, стр. 284 — 285. В написании окончательной формулы Лобачевском мы заменяем синусы параллаксов углами. косинусы — единицей. Заметим, что по 1-й теореме Лобачевского р' не может быть равно нулю.
- 18. Эту ошибку обнаружил впервые проф. Энгельс в его комментированном немецком издании «О началах геометрии»; см. Н. И. Лобачевский, т. 1. Комментарий, стр. 286.
Добавить комментарий