Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
5. Условие одновременной измеримости двух физических величин.
Нам известно, что физическая величина изображается некоторым эрмитовым оператором, и что она может принимать с некоторыми вероятностями те или иные значения.
И лишь в тех состояниях, которые описываются собственными векторами оператора физической величины, физическая величина принимает некоторые вполне определённые значения.
В связи с этим возникает вопрос, при каком условии две физические величины принимают определённые значения, т.е. одновременно измеримы?
Докажем утверждение:
Две физические величины могут быть одновременно измеримы тогда и только тогда, когда операторы этих физических величин коммутируют.
Пусть величины и
одновременно измеримы, т.е. существует некоторое состояние |х›, в котором эти величины имеют некоторые определённые значения А и В соответственно. Тогда, принимая во внимание линейность операторов, получаем:
|х› =
В|х› = В
|х› = ВА|х›= АВ|х›= А
|х› =
А|х› =
|х›.
Отсюда
Наоборот, пусть
.
Запишем это равенство, например, в – представлении, где оператор
диагонален, тогда
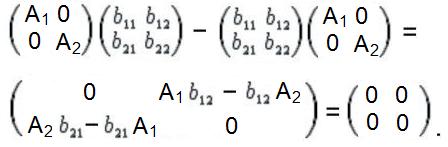
Равенство выполняется автоматически, если А1 = А2 . При А1 ≠ А2 необходимо дополнительно потребовать, чтобы b12 = b21 = 0.
Т.е. матрица оператора должна быть диагональной одновременно с матрицей оператора
. И тогда собственные функции оператора
совпадут с собственными функциями оператора
. В состояниях, описываемых этими собственными функциями, обе физические величины имеют некоторые определённые значения.
6. Соотношения для операторов спина ½.
Все соотношения можно вычислить непосредственно. Например:
= (ħ2/4) (|z +›‹z–| + |z–›‹z+|)(|z +›‹z–| + |z–›‹z+|)=
(ħ2/4) (|z +›‹z–|z +›‹z–| + |z +›‹z–|z–›‹z+| + |z–›‹z+|z +›‹z–| +|z–›‹z+|z–›‹z+|) =
(ħ2/4) (0·|z +›‹z–| + 1·|z +›‹z+| + 1·|z –›‹z–| + 0·|z –›‹z+|) =
(ħ2/4) (|z +›‹z+| + |z –›‹z–|) = (ħ2/4).
Или же можно воспользоваться соответствующими соотношениями для σ–матриц Паули. И получаем:
= (ħ2/4)
,
= (ħ2/4)
.
Отсюда
Операторы ,
,
антикоммутируют:
здесь — нулевой оператор, который изображается в любом представлении квадратной матрицей 2х2, состоящей лишь из нулей.
Коммутационные соотношения таковы:
Обратите внимание на то, что оператор пропорционален тождественному оператору
. Поэтому его действие сводится лишь к умножению справа или слева на число
.
Т.е. коммутирует с любым оператором
,
,
и, вообще, с оператором
= ħ/2[n
+ m
+ k
] = [n
+ m
+ k
].
Следовательно, особенности квантово–механической системы со спином ½ таковы, что одновременно могут быть измерены лишь две величины: квадрат момента импульса и проекция момента импульса на любое направление.
Одновременно измерить проекции момента импульса хотя бы на две координатные оси невозможно, поскольку ,
,
не коммутируют между собой.
Последние комментарии