Коротко о тригонометрических функциях. I

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

Наверное, есть люди, которые захотят ознакомиться с квантовой механикой, но они совсем не знают тригонометрии и поэтому думают, что квантовая механика для них недоступна.

Но это не так. Тригонометрию действительно нужно знать, но не обязательно знать основательно, достаточно знакомства с азами.

Ниже рассматриваются основные свойства тригонометрических функций, причём лишь самые главные, — только те, что понадобится в дальнейшем.

Слово тригонометрический, тригонометрия произошло от греч. trigonon — треугольник, metro — метрия, и дословно означает измерение треугольников.

Поэтому начнём с рассмотрения самого простого треугольника, — прямоугольного.

1. Теорема Пифагора и одно важное следствие из неё.

Теорема П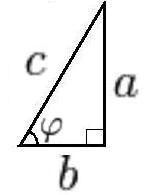ифагора справедлива лишь для прямоугольных треугольников, т.е. для треугольников, у которых один угол прямой, а остальные два — острые:

Пусть катеты a и b лежат напротив острых углов, гипотенуза c лежит напротив прямого угла.

Формулировка теоремы Пифагора: площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах:

a² + b ² = c ²

Простейшее доказательство теоремы Пифагора:

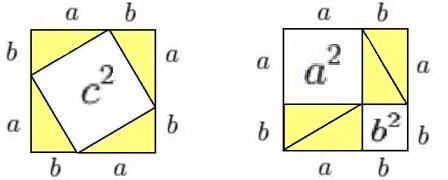
Из двух равновеликих квадратов площадью (a + b)² вырезаются четыре одинаковых прямоугольных треугольника (на чертеже они помечены жёлтым цветом). Следовательно, оставшиеся площади (они помечены белым) тоже равновелики. Что и требовалось доказать.

Отсюда получается важное следствие: формула вычисления расстояний между двумя точками А(х₁, y₁) и В(х₂, y₂) на плоскости:

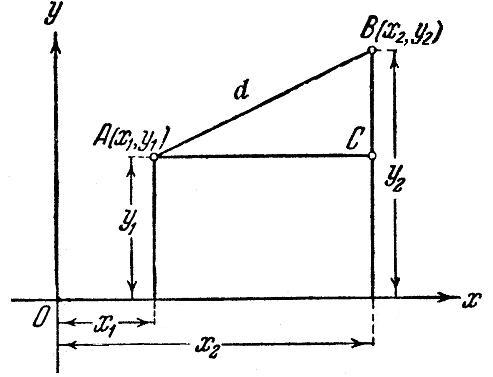
В треугольнике АВС сторона АВ является  гипотенузой, а катеты АС  и ВС соответственно равны  (х₂ – х₁) и (y₂ – y₁).

Поэтому согласно теореме Пифагора квадрат длины гипотенузы АВ вычисляется по формуле:

,

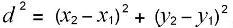и, окончательно:

.

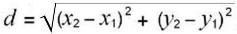2. Определение тригонометрических функций

Тригонометрические функции определяются через отношение катетов друг к другу или к гипотенузе.

Синусом φ называется отношение противолежащего катета к гипотенузе:

Косинусом φ называется отношение прилежащего катета к гипотенузе:

Тангенсом φ называется отношение противолежащего катета к прилежащему:

Котангенсом φ называется отношение прилежащего катета к противолежащему:

Наконец, иногда применяются секанс и косеканс:

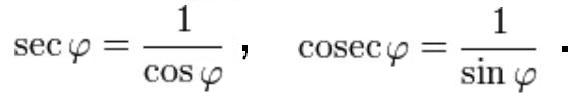
3. Тригонометрические функции 30°, 45° и 60°.

Рассмотрим равнобедренный прямоугольный треугольник, у которого острые углы равны 45°, а гипотенуза равна 1. Обозначим катеты через х, тогда  по теореме Пифагора х ² + х² = 1 и

Разделив х  на длину гипотенузы, т.е. на единицу, получим:

Отсюда тангенс 45° равен котангенсу 45° и равен единице.

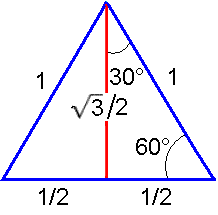Теперь разделим равносторонний треугольник высотой, которая является также и медианой, и биссектрисой, на два прямоугольных треугольника. Пусть гипотенуза прямоугольных треугольников равна 1, тогда один из катетов равен 1/2, а высота, т.е. общий катет, согласно теореме Пифагора, равна

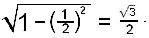
Отсюда легко вычисляются значения всех тригонометрических функций:

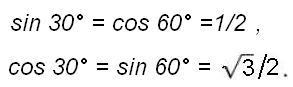
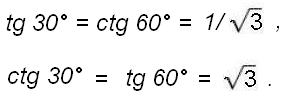
Как мы здесь убедились, заново вычислить тригонометрические функции 30°, 45° и 60° значительно проще, чем навсегда запомнить их значения.

4. Ещё одно важное следствие из теоремы Пифагора.

Вычислим выражение:

Тогда из теоремы Пифагора получаем очень важное равенство:

sin²φ + cos²φ =1.

И это равенство, и приведённые выше определения тригонометрических функций имеют смысл пока лишь для острых углов, потому что в прямоугольном треугольнике все углы, за исключением прямого угла, острые.

Оказывается, возможны обобщения на случай любых углов.

Продолжение.

©   А.А.Дмитриевский.