Участие в деле Миллера на время отвлекло Н. И. Попова от его основной деятельности, поскольку ему пришлось штудировать много книг по русской истории, но астрономию он не забывал [II, 23, т. 10, с. 239]. Развивая свой метод («глаз и ухо»), ранее примененный им к наблюдению затмений, 2 ноября 1750 г. Н. И. Попов представил в Академию наук «Метод для наблюдения кульминаций и азимутов звезд, так же как и их соответствующих высот» [I, 15].
 Новая работа Н. И. Попова вызвала оживленную полемику1, в которой активно участвовал X. Г. Кратценштейн, доказывая, как и раньше, что метод Попова не нов и те же наблюдения можно провести другими способами2. X. Н. Винсгейм, ранее всегда относившийся с симпатией к Попову, теперь (вероятно, после дела Миллера) устранился от обсуждения его работы. В своем отзыве он писал: «Понеже г-н адъюнкт Попов в специмене своем описывает инструмент астрономической и ожидаемую от онаго пользу, то изследование сего инструмента от академического собрания поручено механику г-ну доктору Кратценштейну, понеже прочие господа о такой материи справедливо и основательно рассуждать не могут, а я притом и не в состоянии всходить на обсерваторию и находящейся на оной инструмент изследовать»3. Итак, сославшись на свою некомпетентность и тучность, Винсгейм полностью передал работу Попова на суд его недоброжелателя X. Г. Кратценштейна.
Новая работа Н. И. Попова вызвала оживленную полемику1, в которой активно участвовал X. Г. Кратценштейн, доказывая, как и раньше, что метод Попова не нов и те же наблюдения можно провести другими способами2. X. Н. Винсгейм, ранее всегда относившийся с симпатией к Попову, теперь (вероятно, после дела Миллера) устранился от обсуждения его работы. В своем отзыве он писал: «Понеже г-н адъюнкт Попов в специмене своем описывает инструмент астрономической и ожидаемую от онаго пользу, то изследование сего инструмента от академического собрания поручено механику г-ну доктору Кратценштейну, понеже прочие господа о такой материи справедливо и основательно рассуждать не могут, а я притом и не в состоянии всходить на обсерваторию и находящейся на оной инструмент изследовать»3. Итак, сославшись на свою некомпетентность и тучность, Винсгейм полностью передал работу Попова на суд его недоброжелателя X. Г. Кратценштейна.
Г. В. Рихман более благожелательно отозвался о Попове и его работе. Он предложил дать ученому возможность доказать на практике преимущества своего метода. Только что приехавший из Германии новый профессор астрономии А. Н. Гришов, несмотря на определенное давление со стороны канцелярии, дал уклончивый отзыв, стараясь никого не обидеть: «... не имею я того намерения, чтоб мне г-на адъюнкта в ведомом мне уже давно его искусстве... порочить...»4.
Несмотря на разногласия, И. Д. Шумахер не решился больше обращаться к Л. Эйлеру, высокое мнение которого о методе Н. И. Попова он уже знал. Кроме того, Шумахер не мог не считаться и с возросшим в эти годы влиянием Ломоносова, который полностью поддержал Попова. Это, по-видимому, решило дело. В один и тот же день, 12 марта 1751 г., оба ученых были повышены в чинах: один стал коллежским советником, а второй — профессором астрономии. И. Д. Шумахер сообщил об этих событиях Л. Эйлеру [II, 60, с. 238]. Одобряя оба назначения, Л. Эйлер писал о H. И. Попове: «Г. Попов — несомненно очень искусный астроном, как я увидел из его статей, и астрономия не могла бы быть отныне лучше замещена, если бы только г. Гришов с г. Поповым стали жить в хорошей дружбе» [II, 60, с. 239].
Итак, Н. И. Попов стал третьим профессором астрономии с жалованием 660 руб. в год. В то время это звание приравнивалось к званию академика. 9 марта 1751 г. он был приведен к присяге5. Однако работа Н. И. Попова [I, 15] так и осталась неопубликованной. Вероятно, дело Миллера в какой-то мере повлияло на это решение.
Речь о лунной теории. 7 сентября 1752 г. Н. И. Попову было поручено выступление на публичном собрании Академии наук с речью: «О новых изобретениях в лунной теории» [I, 2]. Собрание было приурочено к представлению в Петербургскую Академию диссертации Л. Эйлера по теории Луны [II, 64]. Она завершила важный цикл исследований, доказавших справедливость учения И. Ньютона. Это учение, лежащее в основе современной небесной механики, в середине XVIII в. переживало глубокий кризис. Первые попытки объяснить движения небесных тел с помощью теории тяготения встретились с такими трудностями, что многие ученые стали сомневаться даже в справедливости закона тяготения.
Для решения вопроса Парижская, Берлинская и Петербургская академии наук провели специальные конкурсы в 1748 — 1751 гг. Наибольшее значение имели исследования А. К. Клеро и Л. Эйлера. Первое [II, 52] было премировано Петербургской Академией, второе [II, 64] — Парижской. Условия конкурсов и представленные на них работы были подробно изучены специалистами [II, 10, 43 и др.], поэтому нет необходимости на них останавливаться.
Публичное собрание 7 сентября 1752 г., подведя итоги этим конкурсам, стало своеобразным торжеством ньютоновского учения. Естественно, что честь выступить с речью на таком собрании была предоставлена Н. И. Попову — ученику двух убежденных ныотонианцев Ж. Н. Делиля и Л. Эйлера. Он осветил историю открытия и изучения неравенств в движении Луны, дав популярную и краткую характеристику наиболее важных из них.
Большое внимание Попов уделил роли Ньютона в создании основ небесной механики, фундаментом которой стали ньютоновы законы механики и закон всемирного тяготения. Указав, что Ньютон дал лишь методы, с помощью которых можно было получить все лунные неравенства, но не провел самих вычислений, Попов остановился на драматической истории проверки истинности учения Ньютона. Неудачи, сомнения, разочарования, результаты знаменитых конкурсов, объявленных Петербургской и Парижской академиями для решения этой задачи, и наконец полное торжество ньютоновой теории, на которой отныне «вся астрономия основание свое имеет», — были весьма живо представлены слушателям.
Затем оратор детально проанализировал работы Л. Эйлера [II, 64] и А. К. Клеро [II, 52], которые убедительно доказали, что «учение Невтоново о свойстве небесных тел с самою истиною совершенно сходствует» [I, 2, л. 55]. Центральное место в речи Н. И. Попова занимало изложение содержания присланной Л. Эйлером работы по теории движения Луны. Работа печаталась в Берлине на средства Петербургской Академии наук. Попову было поручено публично выразить мнение академиков о работе своего знаменитого коллеги. Эта часть речи посылалась на просмотр Л. Эйлеру.
Особое внимание было обращено на практическую ценность исследований по теории движения Луны, благодаря которым удается, как отметил докладчик, «... подлинное Луны место на небе точнее, нежели во все прежнее время, находить, и потому долготу мест земных на сухом пути и на море столько же исправнее определять, от чего ... все свое совершенство география и навигация получить могут» [I, 2, л. 65 об., 66].
В заключение Н. И. Попов с удовольствием отметил плодотворность научного сотрудничества Петербургской и Парижской академий в исследовании лунных неравенств и остановился на планах новых совместных работ по определению параллакса Луны.
Речь Попова была опубликована в том же 1752 г. параллельно на русском и латинском [I, 2, 7] языках. Она стала практически последней его печатной работой по астрономии, не считая некоторых наблюдений. Это обстоятельство было обусловлено рядом причин, главным образом не относящихся к науке. Во-первых, в Академии того периода не оставалось уже столь крупных ученых-иностранцев, как Л. Эйлер, Д. Бернулли или Ж. Н. Делиль, которые могли бы справедливо оценить и поддержать интересные научные идеи. Работавшие же в Петербургской Академии иностранцы — в основном выходцы из Германии, не имевшие еще авторитета в науке, — чувствовали себя в России елизаветинской эпохи весьма неуверенно. Стремясь всеми силами сохранить свое положение в Академии, они нередко поступались интересами науки в своих личных целях.
Во-вторых, пресловутое самоуправство Академической канцелярии достигло в этот период небывалых размеров. Если также учесть, что исключительно от канцелярии зависел вопрос о публикации научных исследований, то неудивительно, что кроме наблюдений и переводов, работы Попова не печатались, поскольку в состав академической администрации входили Шумахер, Тауберт и Миллер. Один Ломоносов, ставший впоследствии членом канцелярии, далеко не всегда мог изменить ход событий.
Однако вся эта сложная обстановка прежде всего отражалась на судьбе тех, кто только начинал свой путь в науку. Многие из них подавали большие надежды, но так и не стали учеными. Например, талантливый математик М. Софронов, проходивший стажировку у Л. Эйлера в Берлине. Другие, наделенные от природы большими способностями, не смогли раскрыть всех своих дарований.
Весьма показателен в этом отношении пример В. Кузнецова — способного студента, начавшего работать на обсерватории незадолго до отъезда Делиля. По распоряжению канцелярии он был отстранен от слушания лекций в университете и направлен работать при Географическом департаменте и обсерватории. В течение ряда лет он вел записи в журнале наблюдений обсерватории и в совершенстве освоил астрономическую практику. Несколько таких журналов с записью разнообразных наблюдений Н. И. Попова, А. Д. Красильникова, В. Г. Кузнецова и других, охватывающих период с 11 ноября 1749 г. по 2 марта 1751 г., хранится в Ленинградском отделении Архива АН СССР [I, 16]. Однако без знания теоретических основ Кузнецов не мог полноценно заниматься наукой. Настойчивости, твердости характера и необходимых душевных сил для борьбы за свое право заниматься наукой, т. е. всех тех качеств, которыми обладал Н. И. Попов, ему, по-видимому, не хватало. 22 мая 1751 г. В. Кузнецов обратился к экзаменовавшей его комиссии, в состав которой входили М. В. Ломоносов, Н. И. Попов, Г. В. Рихман, И. А. Браун, С. П. Крашенинников, А. Н. Гришов, И. Э. Фишер и Ф. Г. Штрубе де Пирмонт, с просьбой назначить его переводчиком, так как «в рассуждении лет своих и недостатков в других науках... в адъюнкты произойти не имеет надежды»6.
Среди студентов, обучавшихся в этот период в Академии, оказались и будущие участники экспедиции в Сибирь для наблюдений редкого астрономического явления — прохождения Венеры по диску Солнца в 1761 г. — Степан Румовский, Фадей Охтенский и Егор Павинский.
Н. И. Попов и другие профессора на экзамене 20 июня 1751 г. отметили, что, например, Румовский, «разумом и понятием превосходит протчих7. Охтенский, хотя «на физические и математические вопросы посредственно ответствовал», а «в словесных и филозофских науках оказал большие успехи», выразил желание обучаться астрономии. Его просьба была поддержана и профессорами. В то же время знания Павинского оказались, как говорилось в протоколе экзамена, «всех хуже». Он заявил, что не хочет учиться и просил определить его для работы в книжную лавку или Кунсткамеру8.
Несмотря на все трудности, которыми так изобиловала жизнь Попова, он продолжал неутомимо работать. В 1753 г. по очередному призыву Ж. Н. Делиля [II, 54] петербургские астрономы наблюдали явление прохождения Меркурия по диску Солнца. Н. И. Попов вел наблюдения в Петербургской обсерватории, А. Д. Красильников — в Москве, а А. Н. Гришов — в Аренсбурге (ныне г. Кингисепп на о. Сааремаа) [II, 60, с. 310]. Результаты всех этих работ стали известны Ж. Н. Делилю, который использовал их в дальнейшем для усовершенствования разработанного им метода наблюдения прохождений планет по диску Солнца и определения расстояния Земли от Солнца — основной астрономической единицы измерения в Солнечной системе.
Большое значение в подготовке к наблюдениям прохождения Венеры по диску Солнца в 1761 г. сыграли так называемые «планетные конкурсы», объявленные Берлинской (1754 г.), Петербургской (1755 г.) и Парижской (1758 г.) академиями [II, 15]. Они касались разработки теории осевого вращения планет и проблемы планетных атмосфер. Последний вопрос особенно заинтересовал М. В. Ломоносова и Н. И. Попова, который, помимо его исследований, вел различные наблюдения в обсерватории, в том числе и совместно с А. Д. Красильниковым Н. Г. Кургановым, В. Г. Кузнецовым и И. А. Брауном. Некоторые результаты наблюдений были опубликованы [I, 8 — 10 и др.].
Попов работал также и в Географическом департаменте9. Он составлял астрономические календари, рассматривал присылавшиеся в Академию проекты календарей [II, 36, т. 2, с. 256, 259] и другие работы, занимался переводами (в том числе и сибирских наблюдений А. Д. Красильникова). Ему было поручено также «наблюдать чистоту российского языка» в издававшемся Академией популярном журнале «Ежемесячные сочинения»10.
Работы по геодезии и практической астрономии. 13 июня 1757 г. Н. И. Попов представил в Академию наук свою первую работу по геодезии, которая осталась неопубликованной. В переводе с латинского полное ее название звучит так: «Очерк геодезии уже обнародованной, и выведенные из нее практические приложения» [I, 17].
В ней детально излагались общеизвестные к тому времени методы геодезических измерений углов, расстояний и площадей, в том числе и для случаев, когда объекты оказывались хотя бы частично недоступными. Подробно описывались необходимые для всех наблюдений приборы — астролябия, мерительная цепь, колышки, гвозди и т. п. Давались инструкции по правильной установке астролябии и колышков, протягиванию цепи, по коррекции перпендикулярности направления колышков и шестов, параллельности мерительной цепи. Было предложено и несколько мелких, но очень важных усовершенствований, в том числе и уровень для контроля за горизонтальностью прямых линий и плоскостей. Попов предлагал установить на плоскости астролябии такой уровень вместо употреблявшейся тогда магнитной стрелки компаса.
Однако эта работа не встретила сочувствия у большинства коллег Н. И. Попова. Г. Ф. Миллер, заменивший отстраненного М. В. Ломоносова на посту директора Географического департамента, не понимал, насколько важны при проведении триангуляции точные геодезические измерения. Попов, как некогда и его учитель Делиль, был обвинен в стремлении к «излишней точности», а работа его «к печатанию не удостоена»11. К счастью, отстранение Ломоносова оказалось временным. Однако после своего восстановления он не решился поднимать вопрос о работе Попова.
Попытка Н. И. Попова предложить геодезическую тему для публичной лекции на 1757 г. также оказалась безуспешной. Академики сочли, что эта тема слишком «низка» для сановных слушателей, которых усердно зазывали на подобные собрания. Возникли опасения, что, послушав «Речь о геометрическом мерянии Земли и о пользе онаго в науках физике, географии и межевом деле» [I, 11], вельможи могут оскорбиться тем, что им самим предлагается проводить геодезическую съемку и картографирование своих земель. Кроме того, стиль работы Попова также показался всем слишком «низким», простым.
Речь была отклонена. Таким образом, работа, издание которой могло бы принести большую пользу в обучении и практической деятельности геодезистов и картографов, осталась ненапечатанной. Однако Попов широко использовал материалы своей работы для обучения студентов и геодезистов. С 9 ноября 1758 г. по 14 июля 1759 г. он читал студентам Географического департамента и университета, «которые геометрию и тригонометрию разумеют», курс лекций по геодезии и практической астрономии, «сколько исправному геодезисту ... знать надлежит»12.
Первоначально предполагалось, что лекции займут не более двух месяцев и включат лишь практическую астрономию, т. е. методы определения астропунктов и триангуляционной съемки. Однако на первом же занятии выяснилось, что студенты не знают и азов этой науки. Пришлось начать е топографической съемки.
Четыре раза в неделю, окончив ежедневные наблюдения Солнца в обсерватории, они собирались по вечерам на квартире профессора. Для занятий им выдали книги, инструменты и пуд свечей. Помня о своих трудных и голодных ученических годах, он, вероятно, и предложил проводить занятия у себя дома, чтобы хоть немного подкормить студентов и дать им отдохнуть душой в уютной семейной обстановке. В 1750 г. Н. И. Попов женился, в том же году у него родился сын Дмитрий [II, 8, 50].
Геодезия в то время еще не стала самостоятельной наукой, и учебников, тем более на русском языке, не было. Н. И. Попов написал такой учебник, использовав в нем свою неопубликованную работу по геодезии и разработав специальный раздел по высшей геодезии, или, как он ее называл, «практической дорожной астрономии». 16 июня 1759 г. Попов рапортовал Академии: «... понеже такой книги или науки геодезической ... нигде я найти не мог, да уповаю, что и действительно оной еще нет на свете, то я должен был такую науку сам сочинить, ... что я и зделал... и сие великое дело, предложив оное на российском письме моим слушателям, окончал ... 14-го числа текущего сего июля месяца»13.
Вероятно, это был первый учебник геодезии на русском языке, необходимость и своевременность появления которого прекрасно понимал и сам Попов, что видно из того же рапорта Академии: «По сему разсуждаю надобность в обществе человеческом, а паче в российском нашем народе сих моих лекций...»14.
Учебник Н. И. Попова не был опубликован, и рукопись его на русском языке не сохранилась15. Остались лишь латинские варианты. Первый раздел, несомненно, основан на «Конспекте геодезии...» [I, 17]. Второй раздел «Практическая дорожная астрономия» включал предложенный Поповым новый метод быстрой и точной установки инструмента в плоскости меридиана места16 и способ определения разности долгот удаленных друг от друга пунктов без использования астрономических таблиц17. Латинский вариант этой работы под названием: «Метод практической, особенно дорожной, астрономии» [I, 24] был представлен Н. И. Поповым 10 января 1763 г., но также остался неопубликованным.
Завершив чтение лекций, 16 июля 1759 г. Попов предложил провести полевую практику со своими слушателями. Он хотел продолжить начатую Ж. Н. Делилем в 1737 — 1739 гг. триангуляцию, связав обсерваторию с Дудоровой горой. Параллельно с нивелировкой этих пунктов геодезическими методами он предложил определить их высоты барометрическим методом, разработанным Я. Германом в его «Форономии», а заодно и проследить изменение атмосферной рефракции на обсерватории и Дудоровой горе, как некогда предлагал Ж. Н. Делиль. Для проведения практики Попов просил два квадранта радиусом в 2,5 фута «с микрометрами в трубах»18, которые Ж. Н. Делиль считал наиболее удобными для геодезических работ, и другие инструменты. Однако канцелярия не спешила одобрить эти планы. Разрешение было дано лишь 28 августа 1759 г. «Для поздняго времени и худой погоды» практику пришлось отложить на следующее лето19. В дальнейших документах о ней не упоминается.
Работы по математике. Еще с ученических лет Н. И. Попов проявлял интерес к математике. Его способности к этой науке постоянно отмечались как в гимназии, так и в университете, где он с увлечением слушал лекции самого Л. Эйлера, особенно хвалившего его за успехи в алгебре. Интерес к математике Попов сохранил на всю жизнь. Это помогло ему сначала стать неплохим переводчиком математических сочинений, а затем и хорошим вычислителем.
По-видимому, его математические способности ценило и академическое начальство, так как именно ему нередко поручались переводы математических работ. Так, 17 января 1746 г. он переводил математические диссертации для очередного тома «Комментариев» [II, 36, т. 2, с. 109, 110], а в дальнейшем для того же издания составлял резюме работ по астрономии и математике [II, 36, т. 2, с. 208, 234, 235 и др.].
Н. И. Попов много сделал также для подготовки и издания русских учебников по математике. Он, например, редактировал первый русский учебник по алгебре, написанный крупным военным инженером Н. Е. Муравьевым и опубликованный в Петербурге в 1752 г. под названием: «Начальные основания математики» [II, 25, 48 с. 81]. Он принял непосредственное участие и в переводе на русский язык с немецкого второй части книги Л. Эйлера: «Руководство к арифметике для употребления в гимназии при императорской Академии наук». В 1738 — 1740 гг. она издавалась на немецком языке, и возможно что Попов сам по ней учился. Первая часть книги в русском переводе В. Е. Адодурова вышла в 1740 г. [II, 47], а перевод второй ее части был поручен 21 января 1750 г. студенту В. Г. Кузнецову [II, 23, т. 10, с. 449]. Тот, вероятно, не мог разобраться в языковых, а главное в математических трудностях. Попов помог ему, «обучал его алгебре», правил и дополнял перевод [II, 23, т. 10, с. 239, 663 и др.], который наконец и был издан в 1760 г. [II, 47].
Н. И. Попов активно участвовал в обсуждении всех присылавшихся в Академию математических работ. Отзывы на две из них не совпали с мнением Л. Эйлера, что резко изменило судьбу Попова. Работа почетного члена Петербургской Академии наук Г. Кюна: «Размышления о составлении мнимых чисел и извлечении мнимых корней» [II, 36, т. 2, с. 235 и др.] после оживленного обсуждения в 1750 — 1751 гг. была напечатана, несмотря на возражения Л. Эйлера [II, 69]. Решение о ее публикации было принято большинством голосов. Лейпцигский ученый Д. Г. Рудольф был рекомендован на место профессора математики в Петербург и в 1753 г. прислал свое пробное сочинение о среднем пропорциональном. Л. Эйлер дал резкий отзыв на эту работу, и Рудольф не был приглашен, хотя большинство петербургских профессоров сочло отзыв Л. Эйлера чересчур резким [II, 36, т. 2, с. 306 и др].
Эти факты умело использовал Г. Ф. Миллер, который 26 февраля 1754 г. был назначен конференц-секретарем20 и получил в свое распоряжение документы Академической конференции. 6 мая 1755 г. он послал Эйлеру письменные отзывы Попова о работах Рудольфа и Кюна [II, 60, с. 85], снабдив их подробными комментариями о неуважении их автора к мнению Л. Эйлера. Миллеру удалось ввести Эйлера в заблуждение, убедив его в том, что именно отзывы Попова сыграли решающую роль в публикации работы Кюна и смягчении резкого отзыва о работе Рудольфа. Миллер добился того, что в свое время не удалось Шумахеру. Он получил письмо Л. Эйлера от 23 мая 1755 г. с неодобрительным отзывом о Попове [II, 60, с. 87], которое сразу же стало известно всему ученому миру Петербурга. И это не замедлило сказаться на судьбе Н. И. Попова. С этого времени Л. Эйлер больше не защищал его от Академической канцелярии и, по-видимому, надолго сохранил к нему неприязненное чувство.
Однако Н. И. Попов по-прежнему глубоко уважал Л. Эйлера и продолжал с увлечением заниматься задачей о квадратуре круга, которой великий математик посвятил много работ и выступлений в бытность свою в Петербурге [II, 49]. По-видимому, они произвели глубокое впечатление на Попова, к тому же и другие петербургские ученые увлекались этим вопросом. Так, в 1751 г. была напечатана работа Г. В. Крафта, предложившего два метода спрямления окружности, с помощью которых он получил приближенные значения числа π — отношения длины окружности к ее диаметру [II, 68].
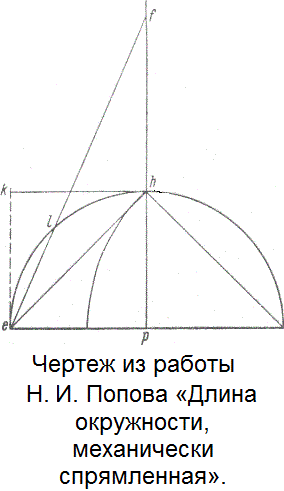 Н. И. Попов, много занимаясь вычислениями с помощью тригонометрических таблиц, прекрасно понимал важность получения более точного значения π. Этому вопросу была посвящена его первая и единственная работа по математике, которую он представил Академии 31 октября 1757 г.: «Длина окружности, механически спрямленная» [I, 18].
Н. И. Попов, много занимаясь вычислениями с помощью тригонометрических таблиц, прекрасно понимал важность получения более точного значения π. Этому вопросу была посвящена его первая и единственная работа по математике, которую он представил Академии 31 октября 1757 г.: «Длина окружности, механически спрямленная» [I, 18].
Геометрическое построение, с помощью которого Попов получил π ≈ 3.14159221, основывалось на следующей доказанной им теореме: «... площадь сегмента четверти круга... относится к площади смешанной фигуры hlekh, ее описывающей, как хорда eh к радиусу круга ер или hk» [I, 18, л. 3 об.]. Пользуясь этой теоремой, как он показал, легко с помощью простых геометрических построений делить сегмент круга на 8, 16 и т. п. число частей. Простота и наглядность делали построение Н. И. Попова «полезным для студентов» и позволяли иллюстрировать лекции по математике. Однако и эта работа осталась неопубликованной. Возможно, что она все же использовалась для обучения.
- 1. Работа обсуждалась на двух заседаниях (2 и 5 ноября 1750 г.) [II, 36, т. 2, с. 246] и 18 января 1751 г. была сдана в Архив [II, 36, т. 2, с. 251].
- 2. ЛО ААН, P. I, № 90, л. 1 — 5.
- 3. Там же, ф. 3, oп. 1, № 146, л. 369.
- 4. Там же, л. 384 об.
- 5. Там же, л. 386 — 388.
- 6. Там же, № 153, л. 327.
- 7. Там же, л. 325.
- 8. Там же, л. 326 об., 327.
- 9. С 1752 г. Географический департамент возглавлял Г. Ф. Миллер, которому 21 февраля 1751 года было возвращено профессорское звание (ЛO ААН, ф. 3, oп. 1, № 149, л. 402).
- 10. ЛО ААН, ф. 3, оп. 1, № 252, л. 4.
- 11. Там же.
- 12. Там же, № 219, 228, 229.
- 13. Там же, 228 об.
- 14. Там же.
- 15. Не исключено, что рукопись была использована при издании в 1766 г. учебника геодезии С. К. Котельникова [II, 16].
- 16. Меридиан места — линия, проходящая через зенит, надир и оба полюса. Она совпадает с направлением тени от вертикального шеста в истинный полдень.
- 17. ЛО ААН, ф. 3, oп. 1, № 219, л. 228, 228 об.
- 18. Там же, л. 229 об.
- 19. Там же, л. 230, 231.
- 20. Там же, ф. 1, оп. 2 — 1754 г., л. 934.
- 21. Напомним, что современное значение π = 3,1415926535897932384626… . Г. В. Крафт получил два гораздо менее точных значения π = 3,141587 и π = 3,141296 [II, 68].
Добавить комментарий