Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
15. Обращение линейного преобразования в простейшем случае.
Чтобы обратить линейное преобразование, нужно, чтобы число аргументов было равно числу функций.
Вот простейший пример, когда это требование нарушается:
![]()
Зная аргументы, можно однозначно вычислить функцию. А, наоборот, однозначно восстановить аргументы по значениям функции невозможно.
На языке матриц это означает, что обращение допускают лишь квадратные матрицы.
Рассмотрим вопрос об обращении матриц подробнее.
Пусть дано линейное преобразование
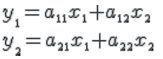
преобразующее пару чисел ![]() в пару чисел
в пару чисел ![]() . Соответствующая матрица имеет вид:
. Соответствующая матрица имеет вид:
Возникает вопрос, возможно ли обратное преобразование
![]() ?
?
Чтобы ответить на этот вопрос, умножим первое уравнение на ![]() , а второе уравнение на
, а второе уравнение на ![]() , а затем исключим
, а затем исключим ![]() из формул линейного преобразования:
из формул линейного преобразования:
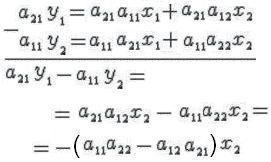
Аналогично, умножая первое уравнение на ![]() , а второе уравнение на
, а второе уравнение на ![]() и исключая
и исключая ![]() из формул, получаем:
из формул, получаем:
![]()
Итак, обратное преобразование имеет следующий вид:
![]()
![]()
Отсюда понятно, что обратное преобразование возможно, при условии, что некоторое число, а именно, ![]() .
.
Это число называется определителем или, иначе, детерминантом матрицы и, в отличие от матрицы, которая изображается с круглыми скобками, определитель ограничен двойными прямыми линиями, но чаще всего одиночными прямыми линиями:
![]()
Итак, обратное преобразование принимает вид:
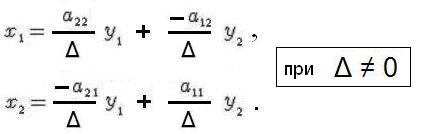
Отсюда получаем обратную матрицу:
16. Правила вычисления определителей.
А теперь сформулируем правила вычисления определителей, которые понадобятся в дальнейшем.
Правило вычисления определителя второго порядка для квадратной матрицы 2х2
![]()
очень простое:
К понятию определителя третьего порядка можно прийти, рассматривая линейное преобразование с тремя аргументами и тремя функциями, подобно тому, как только что было обращено линейное преобразование с двумя аргументами и двумя функциями. Вычисления довольно громоздкие, поэтому они опущены.
Оказывается, что определитель третьего порядка представляет собой выражение:
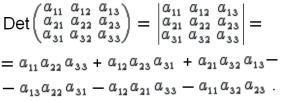
Столь громоздкую формулу для вычисления определителя 3-го порядка можно восстановить с помощью правила Саррюса:
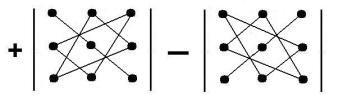
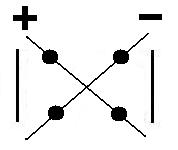
Согласно этому правилу есть три слагаемых со знаком плюс:
— произведение элементов, расположенных на главной диагонали , т.е. диагонали, направленной от левого верхнего угла к правому нижнему углу,
— два произведения элементов, расположенных по ходу треугольников, одна из сторон которых параллельна главной диагонали.
Ещё три слагаемых, берутся со знаком минус; они получаются аналогично, исходя из второстепенной диагонали.
Определители более высоких порядков вычисляются приведением по определённым правилам, которые мы здесь не изучаем, к определителям более низкого порядка. В конечном итоге все определители сводятся к определителям второго и третьего порядка.
Более подробно обращение матриц, правила вычисления определителей высоких порядков мы изучать не будем. Потому что в подавляющем большинстве случаев придётся обращать особые матрицы: ортогональные, унитарные. Их обращение сводится к применению довольно простых операций. А определители высоких порядков нам встречаться не будут.
17. Свойства обратных матриц.
Квадратная матрица называется невырожденной, если её определитель не равен нулю (Δ ≠ 0), и вырожденной, если он равен нулю (Δ = 0).
Выше был получен следующий результат: только невырожденные квадратные матрицы 2х2 допускают обращение.
Оказывается, что это свойство обратных матриц дословно обобщается на случай любых квадратных матриц.
Теперь возникает вопрос коммутирует обратная матрица с исходной, или нет?
Допустим, что не коммутирует, это значит, что для некоторой невырожденной квадратной матрицы ![]() существуют две обратные матрицы,
существуют две обратные матрицы, ![]() и
и ![]() , такие, что
, такие, что
![]() и
и ![]() .
.
Умножим первое из этих выражений на ![]() :
:
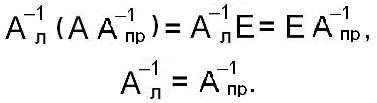
Пришли к противоречию с исходной посылкой о неравенстве левой и правой обратных матриц.
Противоречие означает ложность исходной посылки.
Из того, что левая и правая обратные матрицы совпадают, следует, что обратная матрица коммутирует, т.е. перестановочна с исходной:
![]()
18. Две полезные теоремы.
18.1. Об определителе транспонированной матрицы.
Det A = Det AT
Определитель матрицы в результате её транспонирования не менняется.
18.2. Теорема умножения определителей.
Det (AВ) = Det A · Det В
Определитель произведения двух матриц равен произведению определителей этих матриц. Данное утверждение очевидным образом обобщатся на случай любого числа матриц.
Эти теоремы нам понадобятся в дальнейшем. Что касается их доказательств, то очень простые доказательства мне неизвестны, поэтому теоремы придётся принять на веру.
Впрочем, истинность этих теорем в случае квадратных матриц второго порядка устанавливается непосредственно.
19. Похвальное слово линейной алгебре
В конечном итоге основательного знакомства с линейной алгеброй, где изучаются матрицы, определители, системы линейных уравнений, всевозможные линейные пространства и многие, многие другие полезные вещи, не избежать.
И вообще, линейная алгебра, наряду с математическим анализом, является базовым математическим курсом, которым должен хорошо владеть любой математик, физик и инженер.

Последние комментарии