Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
12. Матричные выражения.
После того, как операции с матрицами определены, из матриц можно составлять различные выражения.
Например: выражение
![]()
где
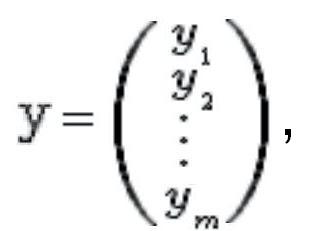

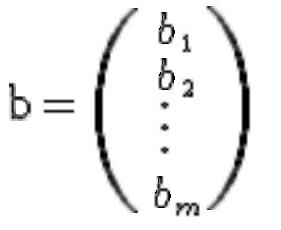
является очень краткой и экономной записью любого неоднородного линейного преобразования, содержащего аргументов,
функций и
свободных членов:
где и
![]() — коэффициенты при аргументах и свободные члены соответственно,
— коэффициенты при аргументах и свободные члены соответственно, ,
.
13. Транспонирование матричных выражений
Нетрудно непосредственно убедиться, что операция умножения матрицы на число или операция вычисления суммы (разности) матриц перестановочны с операцией транспонирования.
Т.е. можно сначала умножить матрицу на число, а потом транспонировать результат, или можно сначала транспонировать матрицу, а затем умножить её на то же самое число. — Результат будет одинаков.
Или можно сначала сложить две матрицы, а затем транспонировать результат, или можно сначала транспонировать матрицы, а потом их складывать. — Результат тоже будет одинаков.
Что касается умножения матриц, то здесь ситуация иная.
Обратимся к схеме умножения матриц и рассмотрим произведение АВ:
При перемножении столбцов не важно, какой столбец стоит справа, а какой слева, поэтому поменяем матрицы местами:
Из правила умножения матриц понятно, что левым множителем матрицы АТ должна быть такая матрица, которая при транспонировании даст матрицу В. Следовательно, это матрица ВТ.
Итак, можно умножать или АВ, или ВТ АТ, матричные элементы получаются одинаковые.
Теперь рассмотрим матричный элемент произведения АВ, расположенный в p-ой строке и q-м столбце. Это значит, что этот элемент получился при перемножении p-ого столбца матрицы АТ и q-ого столбца матрицы В.
После перестановки матриц местами окажется, что теперь этот матричный элемент расположен в p-м столбце результата и, очевидно, в q-ой строке. Т.е. строки и столбцы поменялись местами, Иначе говоря, произведение АВ стало транспонированным.
И, получаем окончательно:
(АВ)Т = ВТ АТ .
Итак, при транспонировании произведений матриц необходимо сначала транспонировать матрицы-сомножители, а затем записать их в обратном порядке.
В качестве примера транспонируем матричное выражение:
![]()
Получаем:
здесь теперь не матрицы-столбцы, а матрицы-строки.
Естественно, что и исходное, и транспонированное матричное выражение изображают одно и то же линейное преобразование.
14. Действия с матрицами, итоги:
Если бы вы изучали систематический курс матричного исчисления, то наверняка узнали бы много разных слов, вроде «ассоциативность сложения и умножения матриц», «дистрибутивность умножения матриц относительно сложения» и т.п., а также встретились бы с формулами, подробно расписывающими свойства операций с матрицами.
Например, с такими:
I. Операции сложения матриц и умножения матрицы на число обладают следующими свойствами (при условии, что такие операции возможны):
1. А + В = В + А;
2. А + (В + С) = (А + В) + С;
3. А + 0 = А;
4. А – А = 0;
5. 1 ∙ А = А;
6. α (А + В) = αА + αВ;
7. (α + β)А = αА + βА;
8. α(βА) = (αβ)А,
II. Операции умножения матриц и транспонирования матричных выражений обладают следующими свойствами (при условии, что такие операции возможны):
1. А(ВС) = (АВ)С;
2. А(В + С) = АВ + АС;
3. (А + В)С = АС + ВС;
4. α(АВ) = (αА)В;
5. А ∙ 0 = 0; 0 ∙ А = 0;
6. А ∙ 1 = 1 ∙ А = А;
7. (α А)Т= α АТ = АТ α;
8. (АВ)Т = В ТАТ;
9. (АВС)Т = СТВТАТ;
10. (А + В)Т = АТ + ВТ .
здесь А, В и С — любые произвольные матрицы, 1 и 0 — единичная и нулевая матрица соответственно, α и β — произвольные числа.
Обратите особое внимание на первую формулу из второй группы:
А(ВС) = (АВ)С.
Она выражает ассоциативность матриц относительно умножения. Это значит, что можно сначала вычислить произведение ВС, а затем слева умножить на А, или сначала вычислить (АВ), а потом справа умножить на С, — результат будет одинаков. И, вообще, матрицы в любом их произведении можно группировать как угодно.
Все перечисленные формулы легко доказываются.
Но при начальном знакомстве с матрицами не морочьте себе всем этим голову.
Потому что с матрицами можно обращаться так же как с привычными для нас числами, за исключением нескольких различий, о которых необходимо помнить:
— сумма, разность и произведение матриц существует не всегда,
— деление матриц не определено,
— произведение квадратных матриц чаще всего не коммутативно,
— единичная матрица при умножении играет в матричном исчислении такую же роль, как число 1 при аналогичных действиях с числами,
— нулевая матрица играет в матричном исчислении такую же роль, как число 0 при аналогичных действиях с числами,
— при транспонировании произведения матриц, нужно не только транспонировать каждую матрицу, но, кроме того, необходимо сменить порядок следования матриц–сомножителей на противоположный.
Последние комментарии