Описание направлений и поворотов в трёхмерном пространстве. VII

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

Назад

14. Спиноры.

Оказывается, кроме рассмотренных выше, есть ещё один способ описания направлений и поворотов в двумерном комплексном евклидовом пространстве.

Исходим из того, что направление в трёхмерном пространстве задаётся матрицей-столбцом d

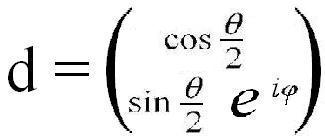
элементы которой в общем случае будем обозначать обозначим через ψ¹ и ψ².

Повороты трёхмерного евклидового пространства представлены в двумерном комплексном пространстве унитарными матрицами

U_X(α/2) = Е cosα /2 + iσ_x sinα /2,

U_Y(α/2) = Е cosα/2 + iσ_y sinα/2,

U_Z(α/2) = Е cosα /2 + iσ_z sin/2

или любыми их произведениями. Для всех таких матриц, обозначим их через U, характерно, что они являются унитарными с определителем, равным единице, Δ = 1.

Пусть

тогда новые матричные элементы после поворота будут выражаться формулой:

d′ = Ud,

В принятых обозначениях это равенство имеет вид:

чему соответствует линейное преобразование

(ψ¹)′ = αψ¹ + βψ²

(ψ²)′ = γψ¹ + δψ².

Обратим матрицу U, воспользовавшись готовым результатом (см. Просто и доступно о матрицах. VI). Для этого элементы  главной диагонали следует поменять местами, а элементы  второстепенной диагонали нужно умножить на –1, кроме того, полученную матрицу следовало бы разделить на определитель Δ, но Δ = 1. И тогда, учитывая унитарность матрицы U, получим:

.

Матрица-строка d^† с элементами (ψ¹)* и (ψ²)* при повороте преобразуется согласно формуле:

(d^†)′ = d^†U^†,

или 

(d^†)′ = d^†U^–1.

Сменив обозначения,

χ₁ = (ψ¹)*,  χ₂ = (ψ²)* ,

распишем последнюю формулу (d^†)′ = d^†U^–1 подробно:

.

Это соотношение эквивалентно линейному преобразованию:

χ₁′ = δχ₁  – γχ₂,        

χ₂′ = – βχ₁ + αχ₂.        

Отсюда получаем:

Итак, в двумерном комплексном евклидовом пространстве есть два типа объектов, описывающих направления в трёхмерном евклидовом пространстве, — контравариантные и ковариантные спиноры, а пространство в таком случае называется спинорным.

Контравариантные спиноры при поворотах преобразуются по формуле:

Ковариантные спиноры при поворотах преобразуются по формуле

или

.

Два последних матричных равенства взаимно транспонированные.

Далее вводится скалярное произведение одного ко- и одного контравариантного спинора:

[χ , ψ] = χ₁ ψ¹ + χ₂ ψ².

Скалярное произведение является инвариантом относительно поворотов:

,

поскольку Δ = αδ – βγ = 1.

Дальнейшее развитие теории спиноров приводит к спинорному исчислению, которое находит широкое применение в математике и теоретической физике.

Назад

© А. А. Дмитриевский