Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
6. Тригонометрическая форма комплексных чисел.
Пусть дано некоторое комплексное число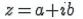 
с модулем 
Очевидно, что 
причём 
Известно, что 
Поэтому существует некоторый угол 
, такой что
В результате получаем тригонометрическую форму комплексных чисел:
Угол называется аргументом комплексного числа.
Нам уже известно, что комплексные числа являются матрицами следующего вида:
Подставив сюда 
получим:
.
7. Геометрический смысл линейного преобразования, соответствующего комплексному числу в матричной форме.
Выясним геометрический смысл аргумента комплексного числа.
Только что нами получена матрица, изображающая любое комплексное число. Запишем соответствующее ей линейное преобразование, рассматривая при этом частный случай 
:
Пусть даны две точки 
и 
. Линейное преобразование переводит эти точки в 
и 
соответственно.
Вычислим расстояние 
Скобки в подкоренном выражении равны:
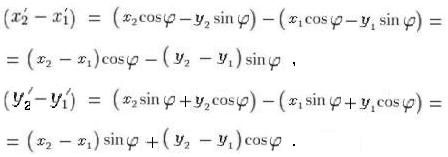
Теперь вычислим сумму квадратов:
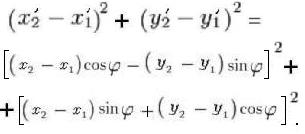
Удвоенные произведения здесь взаимно уничтожаются, поэтому
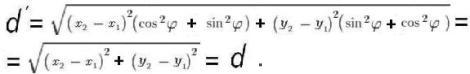
Это значит, что исследуемое линейное преобразование таково, что все расстояния сохраняются.
Для равенства треугольников необходимо и достаточно, чтобы были равны их стороны. Поэтому линейное преобразование преобразует любой треугольник в некоторый треугольник, равный исходному. Следовательно, в результате линейного преобразования сохраняются не только расстояния, но и углы.
Кроме того, непосредственно убеждаемся, что начало координат остаётся неизменным, иначе говоря, точка (0,0) переходит в точку (0,0).
Преобразование плоскости называется поворотом плоскости вокруг центра, если оно сохраняет расстояния и углы и, кроме того, оставляет низменной некоторую точку, называемую центром поворота.
Теперь возьмём произвольный треугольник с вершиной в начале координат. Рассматриваемое нами линейное преобразование преобразует его в точно такой же треугольник и тоже с вершиной в начале координат. Это значит, что, во-первых, произошёл поворот на некоторый угол относительно начала координат, и, во-вторых, все радиусы, исходящие из начала координат поворачиваются на один и тот же угол.
Теперь выясним, какой это угол.
С помощью формул поворота плоскости непосредственно убеждаемся, что точка (1, 0) переводится в точку 
:
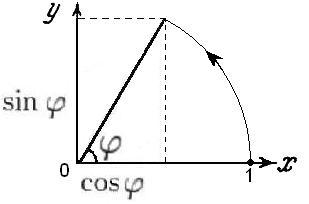
Следовательно, поворот выполняется на угол .
Итак, поворот плоскости относительно начала координат на угол описывается формулами:
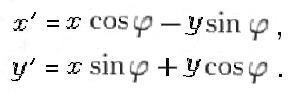
Это значит, что комплексное число
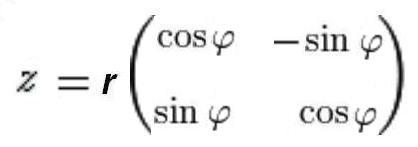
при изображает поворот плоскости против часовой стрелки на угол . Такое направление принято считать положительным.
Если 
, то повторяя приведённые выше соображения, получим, что 
, т.е. все расстояния пропорционально увеличиваются (при 
) или уменьшаются (при 
).
Короче, геометрический смысл комплексного числа таков: выполняется поворот всей плоскости на угол , при , и дополнительно выполняется преобразование подобия при .
А теперь вернёмся к матрице поворота на плоскости:
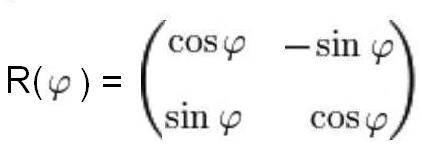
Обратная матрица
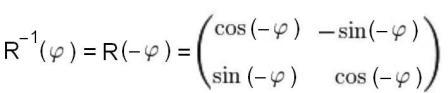
с учётом того, что 
, принимает вид:
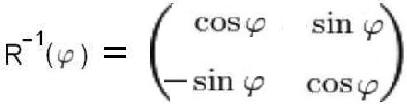
У матриц поворота есть важное и полезное свойство: обратная матрица равна транспонированной:
Матрицы с действительными матричными элементами, у которых транспонированная и обратная матрица совпадают, называются ортогональными.
Определитель матрицы поворота 
равен 1, так как
Можно доказать, что определитель любой ортогональной матрицы равен ±1.
Последние комментарии