Дано: Σ + предложение Пифагора.
Доказать:
1.
Возьмем равнобедренный прямоугольный треугольник с гипотенузой, длина которой равна с, и катетами, длины которых равны a (рис. 11): ∠АСВ прямой, углы А и В острые.
2.
Для доказательства нашего утверждения достаточно показать, что ∠А = ∠В
3.
Опустим перпендикуляр СD из вершины прямого угла на гипотенузу: AD = DB = с/2 (рис. 12).
4.
Применяя предложение Пифагора к прямоугольному треугольнику АВС, находим с =
5.
Отсюда АD
6.
Применяя теперь предложение Пифагора к треугольнику АDС, получим СD
7.
Значит, AD = DC.
8.
Следовательно, ∆ADC
8.
Поэтому ∠А = ∠ACD.
10.
Но ∠ACD =
11.
Поэтому ∠A = 45°.
12.
Но треугольник АВС равнобедренный. Поэтому
13.
Отсюда ∠A + ∠В + ∠С =
Вопрос. Можно ли теперь считать, что теорема доказана?
Подумайте, а затем см. указание 59.
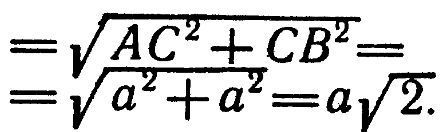
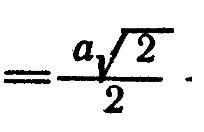
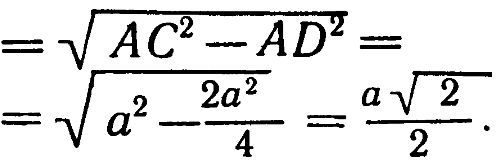
Добавить комментарий