Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
4. Дуальные числа.
Снова вернёмся к матричному уравнению
![]() .
.
Но теперь рассмотрим случай, когда дискриминант равен нулю, ![]() .
.
Выделяем, как обычно, полный квадрат
![]()
и получаем:
![]()
Оказывается, существуют ненулевые матрицы, квадрат которых равен нулю, например:
![]()
В конечном итоге приходим к дуальным числам такого вида:
![]() .
.
Здесь ![]() и
и ![]() некоторые действительные числа.
некоторые действительные числа.
Модуль дуального числа равен ![]() . Он вводится аналогично тому, как вводились модули двойных и комплексных чисел.
. Он вводится аналогично тому, как вводились модули двойных и комплексных чисел.
Алгебраические операции с дуальными числами в точности подобны действиям с комплексными или с двойными числами. Единственное отличие: везде, где встретится ε2, полагаем ε2 = 0.
Деление на дуальные числа вида ![]() , т.е. на те у которых
, т.е. на те у которых ![]() = 0, невозможно, что ограничивает область применимости дуальных чисел по сравнению с комплексными.
= 0, невозможно, что ограничивает область применимости дуальных чисел по сравнению с комплексными.
Тем не менее, и двойные, и дуальные числа всё же нашли своё применение в математике (см. И.М.Яглом Комплексные числа и их применение в геометрии. М.:Физматлит, 1963.).
5. Комплексные числа — это особые матрицы.
Если дискриминант матричного уравнения ![]() то решение уравнения принимает вид:
то решение уравнения принимает вид:
![]()
Из числа, равного минус единице, квадратный корень не извлекается, а из единичной матрицы, умноженной на минус единицу, извлечение корня вполне возможно. Например, ![]() , где
, где
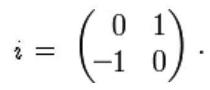
Поэтому решением квадратного матричного уравнения являются матрицы вида
![]()
Единичная матрица при умножении играет роль единицы, поэтому выполняя алгебраические преобразования, можно её вообще опускать. Из равенства ![]() следует, что там где встретится
следует, что там где встретится ![]() , можно просто писать минус единицу.
, можно просто писать минус единицу.
В результате приходим к общепринятой записи вычислений с комплексными числами, — всё точно так, как если бы мы вводили комплексные числа традиционным способом.
Что касается комплексных чисел, то, они применяются настолько широко, что, наверное, будет проще сказать, где они не применяются.
В дальнейшем изложении будут встречаться только комплексные числа.
Комментарии (2)
Минус в матрице
Не баг и не фича
Квадрат матрицы получается согласно правилу умножения матриц, в результате получается единичная матрица, умноженная на минус единицу.
Можно, если хотите, взять в качестве мнимоединичной матрицы такую: в верхней строке 0 и -1, а в нижней 1 и 0. По существу ничего не изменится, потому что квадрат такой матрицы тоже будет равен единичной матрице, умноженной на минус единицу.