Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
9. Способ описания направлений и поворотов с помощью матрицы проектирования.
Нам уже известно, что направление можно задать через половинные углы матрицей–столбцом:
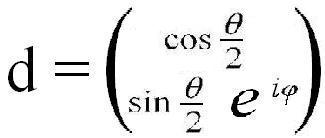 ,
,
а повороты можно описать с помощью любой матрицы U: UХ(φ/2), UY(φ/2) или UZ(φ/2).
Новое направление после некоторого поворота будет задаваться матрицей d′ = Ud.
Очевидно, что матрицу d можно эрмитово сопрягать, т.е. выполнить в любом порядке две операции, — транспонирования и комплексного сопряжения. В результате мы опишем все те же направления и повороты, но лишь слегка по-другому.
Поскольку операция комплексного сопряжения не меняет порядок матриц, а операция транспонирования, наоборот, меняет, то (d′)† = d†U†.
Из матриц d и (d)† можно сконструировать квадратную матрицу d(d)†, которая, также как и исходные матрицы задают направление в трёхмерном пространстве.
Явное выражение для такой матрицы имеет следующий вид:
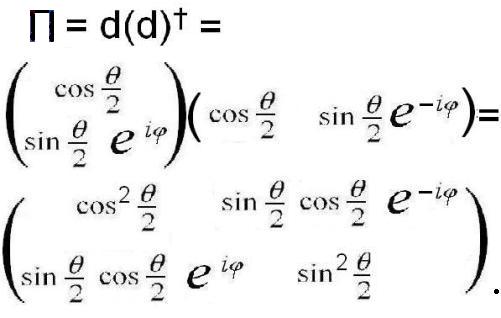
Назовём матрицу П = d(d)† матрицей проектирования, смысл такого названия раскроется позже. Формула её преобразования при поворотах принимает следующий вид:
П′ = d′(d′)† = U dd†U† = UПU†
10. Кватернионы.
Допустим, что в трёхмерном пространстве выполнены два последовательных поворота на произвольные углы вокруг двух разных координатных осей.
В двумерном комплексном пространстве эти повороты будут изображаться произведением каких-то двух матриц из трёх: UX(α), UY(β), UZ(γ).
Непосредственно перемножая эти матрицы попарно, убедимся, с учётом коммутационных соотношений для матриц Паули, что получится выражение следующего вида:
q = a'Е + ib'σx + ic'σy + id'σz ,
здесь a', b', c', d' — некоторые действительные числа.
Это выражение описывает повороты трёхмерного пространства в самом общем виде, потому что если выполнять какие-либо ещё повороты, то общий вид матрицы q останется неизменным, так как произведение двух разных матриц Паули даёт третью матрицу с тем или иным знаком и, кроме того, квадрат любой матрицы Паули равен единичной матрице.
Рассмотрим теперь частный случай b' = d' = 0, тогда q = a'Е + ic'σy. У этой матрицы на главной диагонали — одинаковые действительные числа, а на второстепенной диагонали расположены равные по модулю действительные числа, но с противоположными знаками.
Очевидно, a'Е + ic'σy — старый знакомый, это комплексное число, представленное в матричной форме! (см. Комплексные числа и повороты на плоскости. III). В традиционной форме такое комплексное число записывается так: z = a' + ic' .
Отсюда понятно, что матрица, q = a'Е + ib'σx + ic'σy + id'σz , называемая кватернионом (от лат. quaterni, по четыре), является естественным обобщением комплексных чисел. А именно, здесь не одна мнимая единица, а целых три!
Существенными при выполнении действий с кватернионами оказываются, в конечном итоге, лишь алгебраические свойства матриц iσx, iσy, iσz. Кроме того, единичная матрица при умножении матриц играет роль единицы, поэтому выполняя алгебраические преобразования, её можно вообще опускать.
Будем считать iσx, iσy, iσz мнимыми единицами и обозначим их через i, –j, k соответственно; единичную матрицу Е запишем как обычную единицу. В результате получим традиционную форму записи для кватерниона:
q = a + bi + cj + dk ,
здесь a, b, c, d — некоторые действительные числа.
Обратите внимание на то, что iσy заменяется именно на –j, а не на +j с той целью, чтобы формулы для парных произведений i, j, k были подобными.
Алгебраические свойства мнимых единиц очевидным образом следуют из соответствующих соотношений для матриц Паули:
|
Соотношения для матриц Паули |
Соотношения для мнимых единиц |
|
Квадраты: σx2 = σy2 = σz2 = σ0 = Е |
Квадраты: i2 = j2 = k 2 = –1 |
|
Эрмитовость: σx† = σx, σy† = σy, σz† = σz. |
Комплексное сопряжение: i* = –i, j* = –j, k * = –k. |
|
Парные произведения: 1. σx ∙ σy = iσz , σy ∙ σz = iσx , σz ∙ σx = iσy .
2. σx ∙ σy = – σy ∙ σx , σy ∙ σz = – σz ∙ σy , σz ∙ σx = – σx ∙ σz . |
Парные произведения: 1. i j = k, j k = i, k i = j.
2. ji = – ij = – k, kj = – jk = – i, i k = – k i = – j. |
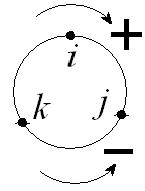 Результат парных произведений мнимых единиц легко восстанавливаются с помощью циклических перестановок согласно рисунку.
Результат парных произведений мнимых единиц легко восстанавливаются с помощью циклических перестановок согласно рисунку.
Последние комментарии