Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
Чтобы скачать полный текст, пройдите по ссылке.
13. Угол между двумя направлениями.
Если даны единичные векторы, задающие два направления через декартовы координаты: x1, y1, z1, r1 = 1 и x2, y2, z2, r2 = 1, то косинус угла между ними вычисляется по формуле (см 13. Угол между направлениями):
cosα = x1 · x2 + y1 · y2 + z1 · z2 .
Теперь запишем то же самое в сферических координатах:
x1 = sinθ1 cosφ1, y1 = sinθ1 sinφ1 , z1 = cosθ1,
x2 = sinθ2 cosφ2, y2 = sinθ2 sinφ2, z2 = cosθ2.
Поэтому
cosα = cosθ1 cosθ2 + sinθ1 sinθ2 cos(φ1 – φ2).
Пусть теперь даны два чисто мнимых (векторных) кватерниона с теми же самыми декартовыми координатами, что и выше.
p1 = x1i + y1j + z1k, r1 = 1,
p2 = x2i + y2j + z2k, r2 = 1.
Перемножая эти два кватерниона, убедимся, что действительная (скалярная) часть произведения не зависит от порядка сомножителей и равна:
Re(p1 p2) = Re(p2 p1) = – (x1 · x2 + y1 · y2, + z1 · z2).
Отсюда
cosα = – Re(p1 p2) = – Re(p2 p1) = x1 · x2 + y1 · y2, + z1 · z2 =
= cosθ1 cosθ2 + sinθ1 sinθ2 cos(φ1 – φ2).
Теперь выразим угол между направлениями через половинные углы. Пусть два направления заданы матрицами вида
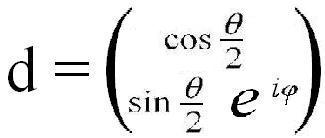 ,
,
а индексами 1 и 2 будем указывать номер направления.
Вычислим сначала самое простое выражение, которое только можно составить из таких матриц, d2†d1:
d2†d1 = cosθ1/2 · cosθ2/2 + sinθ1/2 · sinθ2/2 · exp i(φ1 – φ2),
здесь eхp — ещё одно общепринятое обозначение показательной функции с основанием е ≈ 2,718…
Угол между двумя направлениями является действительным числом, а d2†d1 — число комплексное. Простейшее действительное число, которое можно составить, исходя из d2†d1, имеет следующий вид:
(d2†d1) · (d2†d1)* = (d2†d1) · (d2†d1)† = (d2†d1)(d1†d2) =
[cosθ1/2 · cosθ2/2 + sinθ1/2 · sinθ2/2 · exp i(φ1 – φ2)][cosθ1/2 · cosθ2/2 + sinθ1/2 · sinθ2/2 · exp –i(φ1 – φ2)].
Продолжаем вычисления:
(d2†d1)(d1†d2) = cos2θ1/2 · cos2θ2/2 + cosθ1/2 · cosθ2/2· sinθ1/2 · sinθ2/2·[exp i(φ1 – φ2) + exp–i (φ1 – φ2)] + sin2θ1/2 · sin2θ2/2 =
{(1 + cosθ1)(1 + cosθ2) + sinθ1 · sinθ2 · [cos(φ1 – φ2) + i sin(φ1 – φ2) + cos(φ1 – φ2) – isin(φ1 – φ2)] + (1 – cosθ1) (1 – cosθ2)}/4 =
{1 + cosθ1 · cosθ2 + sinθ1 sinθ2 cos(φ1 – φ2)}/2 = (1 + cosα)/2 = cos2α/2 .
И, в конце концов, убеждаемся, что угол α не зависит от того, какое направление принимается первым, а какое вторым.
Итак,
cos2α/2 = (d2†d1)(d1†d2), = d2†П1d2,
или
cos2α/2 = (d1†d2)(d2†d1), = d1†П2d1.
Здесь П1 и П2 матрицы проектирования для первого и второго направления соответственно.
Последние комментарии